Technical details of my small programs
Contents
- Introduction
- Guides
- Linux (x86, framebuffer)
- TIC-80
- Atari ST
- RISC OS / RPI / RISC PC / Acorn Archimedes (ARM)
- Dreamcast
- DOS (x86, MCGA / VGA)
- Tricks
(p5js/tweet/mastodon)
- Introduction
- Rotating Ortho. Cube (2023, ~230 characters)
- Black filled circle (2024, ~122 characters)
- 2-in-1 square / triangle waveform (2025)
- Iterative Dimetric cube (2025)
- HAKMEM 149 line algorithm (2025)
- HAKMEM 149 quad rasterizer / sprite scaler + rotation (2025)
- HAKMEM 149 rotozoom (2025)
- HAKMEM 149 fractal (2025)
Introduction
Articles documenting my tiny graphics programs
and tricks, best read in order (for Linux) to see
progression.
Most early release names are taken from the Star Control
world, one of my favorite adventure game !
Sources can be found here.
Guides
Articles
- My Linux graphics code golf setup
- Atari 8 bits code setup
- Atari
ST / Falcon graphics code setup and code golf tricks
- Dreamcast
setup
- DOS setup
-
Acorn Archimedes setup
RNG
A pseudorandom
number generator might be useful early on, check out this thread about
tiny PRNG, another good source is this, i used
this one early on in my Linux programs, on modern x86 (~2012)
RDRAND
instruction is also available, good enough random numbers can also
be sourced from RAM etc. sometimes.
LCG
(MCG especially) are probably the smallest ones, they just require
an addition and multiply if the moduli is a power of two, there is
also Xorshift.
A naive and primitive one i used on Halite use a 8 bits
register and an addition (can hardly call that a RNG but it was
good enough for me) : r = (r + 159) & 255
Here is an okay 2^16 moduli 16 bits MCG (taken from here
with multiplier value likely found from this tool) : r = (r * 47989) &
65535
The high bits are better for good values with a small range (0
- 7 here) : n = (r >> 13) & 7
Linux (x86, framebuffer)
2020
2021
- Truespace - 256b
- Flagship - 256b
- Campers - 256b
- QuasiSpace - 128b
- Calculating Space - 256b
- Apollonian - 256b
2022
2023
TIC-80
2021
2022
2023
Atari ST
2025
RISC OS /
RPI / RISC PC / Acorn Archimedes (ARM)
2023
2025
Dreamcast
2025
DOS (x86, MCGA / VGA)
2024
Tricks (p5js/tweet/mastodon)
Introduction
JavaScript / p5js code that i
published on various social media account, no definite size goal
but generally less than 256 characters.
Code of this category is not well size optimized on purpose,
they are more to show interesting short algorithms that i either
discovered on my own or experimented with or intro effect that i
replicated, made them with accessibility in mind so not much arcane
code stuff and it use as few as possible p5js stuff and lib stuff
(software rendering) to be ported / understood easily.
This section is all focused on code golfing tricks so
minimizing code / binary size on specific architectures /
languages, they may also be speed efficient but that was not the
main focus.
Rotating
Ortho. Cube (2023, ~230 characters)

no polygons, all integers orthographic
cube render
w=128;f=0;setup=_=>createCanvas(w,w);draw=_=>{background(0);loadPixels();f+=.1;s=sin(f);c=cos(f);for(i=h=64;i--;)for(y=h;y--;)for(x=h;x--;){dx=32-x;dy=32-y;pixels[h+(dx*c-dy*s)+(((h+dx*s+dy*c)/2+i)<<7)<<2]=255-i*4};updatePixels()}The idea is to show off the algorithm of many intros (i
believe) which render pseudo 3d iso / ortho objects such as
cubes in
very small code, these objects can be built easily without going
the usual way by iterating on an area with center 0,0 and applying
a transform to the x,y; this produce a shape which can be extruded
down (with an additional loop), this method also works with any
complex shapes eg. a labyrinth or a text as long as you generate
them and extrude them.

using logical operators
The shading can be done by using the extrusion loop value and
more fancy shading such as per face shading is also easily possible
by either doing it as a single pass or on a second pass by
rendering the cube into a buffer and using the buffer to isolate
face from pixel color / horizontal position. (or a
combination)

fancy texturing / shading ! (logical operators,
also note the lighting fakery)

composition, stacking and scrolling, almost
like the cool 256b intro Pixel Town by
Digimind,
note here that the shading is only on the side faces, could also be
applied on the upper face which would appear as a cheap
roof
The rendering of multiple objects is also easy with a second
pass, it can be pretty fast also since it is just a bitmap that is
copied over. :)


multiple objects

2d map made of
tiny patterns rendered with isometric projection and highly
extruded ortho objects, wave is just a shading trick, still
fairly small
The best way to map the cubes to the screen is to use this
coordinates transform : x = (x - y) and y = (x + y) / 2
To go full 3D from this is not difficult, it will still stay
tiny and fast, just adds 2D rotation to the coordinates, this will
be equivalent to a forward mapping affine renderer (you might have
to downscale the result to remove sampling holes, this can be done
quite easily with scaling; a right arithmetic
shift) and for perspective just add 3D rotation (with pitch
component), texture mapping can also be added easily with the x and
y coordinates and you will get a
simple quad forward mapping 3D renderer at this point, 4-point
quadrilaterals can also be made by adjusting the loop endpoints
which would end up being comparable to a Sega Saturn / 3DO style
rasterizer although they also go further with algorithms to fill
the sampling holes, it will be a bit tricky compared to a triangles
based rasterizer but it might do the job in size limited context or
if you don't care about optimal performances.
Black filled circle (2024, ~122 characters)
x=y=4e4;setup=_=>createCanvas(512,512);draw=_=>{if(x>0)x-=224;for(i=1e4;i--;)point(256+((x+=y>>8)>>8),256+((y-=x>>8)>>8))}
A way to draw a filled circle with the simplest arithmetic
operations (no multiplication, only addition, subtraction and bit
shifting), this use an
integer variant of Minsky circle algorithm (HAKMEM 149) with
adjustment outside the loop to fill the circle (scale or make it
"unstable"), downscale (fixed point) is used to cover the gaps, the
circle fill is noisy if there is no downscale due to lacks of
precision.
This method
is quite tailored to early x86/ARM CPU instructions
because
the core
Minsky circle algorithm and even the downscale can be implemented
in few instructions with movsx
trick (this explain
the shift by 8), shift and
conditional is great on early ARM due to the single instruction
add/sub + barrel shifter (shift) and conditional instructions so
this can be implemented in few instructions on these
CPU.
It is of
course inefficient (slow) with
the major downside that multiple pixels will be revisited if not
cared for.
Can also be
done without the conditional by replacing the conditional code with
:
y -= y >> 8Cleaner fill can be done by adding
x -= x
>> 8 which act as a regular downscale.The cool
thing is that a variable thickness circle (outward or inward; just
a matter of sign) can be done with the exact same code by moving
one of the line above in the loop (and a spiral can even be done if
the shift is small !) :
let x = 6e4
let y = 0
for (let i = 0; i < 1e4; i += 1) {
x += y >> 8
y -= x >> 8
y -= y >> 16 // perturb the orbit by very small
amount, the shift adjust the thickness, downscaling may be needed
to fill the gaps
//...
}
Note that the
usual way of drawing a filled circle (see below) is already quite
small by looping over a rectangular portion of the screen and
checking if the current point is inside or outside the circle (or
doing it by spans) but it require multiplication.
Here is a
more conventional way (but still tiny !) to draw a filled circle,
color (c) is based on distance from center so not uniform,
s2 is half radius and sl is a shift value that
control the circle radius (shortcut to
avoid more operations; only works
with power of two radius), circle radius can of course be
controlled in a finer way by replacing the shift with a division or
a mul and the two loops could be broken into a single one
:
for (let y = 0; y < s; y += 1)
{
for (let x = 0; x < s; x += 1) {
let cx = x - s2
let cy = y - s2
let c = (cx * cx + cy * cy) >> sl
let i = (x + (y << 9)) << 2 //
512x512 canvas (= explain the shifts)
// full white there means that the point lie
outside the circle radius (so just needs a conditional + constant
for an uniform color circle)
// could be done with single conditional
instruction like a cmov on x86 CPU
pixels[i + 0] = c
pixels[i + 1] = c
pixels[i + 2] = c
}
}
2-in-1 square /
triangle waveform (2025)
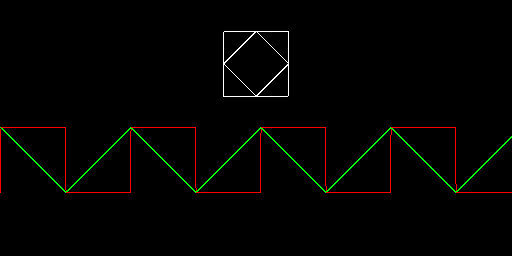
A tiny way to compute a square / triangle wave at
the same time without conditionals, only integers arithmetic and
shifts.
This can be used for oscillators / animations
etc. the algorithm is a variant of HAKMEM
149 and it compute a sine wave approximation when
shifts are not dissimilar.
A square can be made when x and y are both in
use, i also show a diamond shape with a 45° rotation of the
square.
Scaling up X and Y then scaling it down before
drawing can improve precision. (must likely change shifts value
though)
The code below is optimized for size and it has
overdraw.
// -1 also works as a
shortcut (= 256) and -2 allow a precise shape (no missing pixels on
corners)
// but when this value is modified the shifts in the loop below
should also be modified (>> 14 and >> 8 for x=256)
let x = 64 // amplitude and square size
let y = 0
let sw = 512
let sh = 256
let squareSize = x
// draw offset
let shapeOffset = sw / 2 - squareSize / 2 + sh / 8 * sw
let waveformOffset = sh / 2 * sw
for (let t = 0; t < sw; t += 1) { // time
let waveformOffsetX = waveformOffset + t
for (let i = 0; i < squareSize; i += 1) { //
frequency
x += y >> 12
y -= x >> 6
//x += y >> 12 // for extra precision
// scale pass (amplitude)
let px = x
let py = y >> 6
// SQUARE WAVE
let squareWaveformIndex = waveformOffsetX + px *
sw
putPixel(squareWaveformIndex, 255, 0, 0)
// TRIANGLE WAVE
let triangleWaveformIndex = waveformOffsetX + py
* sw
putPixel(triangleWaveformIndex, 0, 255, 0)
// 2D SQUARE
let squareIndex = shapeOffset + px + py * sw
putPixel(squareIndex, 255, 255, 255)
// 2D DIAMOND
let diamondIndex = shapeOffset + ((squareSize -
(px - py) >> 1) + ((px + py) >> 1) * sw)
putPixel(diamondIndex, 255, 255, 255)
}
}
Here is another version for speed with much less overdraw,
only the square wave remains unoptimized due to the sharp
transition :
let x = 64 // amplitude and square
size
let y = 0
let sw = 512
let sh = 256
let squareSize = x
// draw offset
let shapeOffset = sw / 2 - squareSize / 2 + sh / 8 * sw
let waveformOffset = sh / 2 * sw
for (let t = 0; t < sw; t += 1) { // time
let waveformOffsetX = waveformOffset + t
let px = 0
let py = 0
for (let i = 0; i < squareSize; i += 1) { //
frequency
x += y >> 12
y -= x >> 6
// scale pass (amplitude)
px = x
py = y >> 6
// SQUARE WAVE
// note: drawn here to include the sharp
transition; imply overdraw
let squareWaveformIndex = waveformOffsetX + x *
sw
putPixel(squareWaveformIndex, 255, 0, 0)
}
// TRIANGLE WAVE
let triangleWaveformIndex = waveformOffsetX + py * sw
putPixel(triangleWaveformIndex, 0, 255, 0)
// 2D shapes
// SQUARE
let vSquareIndex = shapeOffset + px + py * sw
putPixel(vSquareIndex, 255, 255, 255)
let hSquareIndex2 = shapeOffset + py + px * sw
putPixel(hSquareIndex2, 255, 255, 255)
// DIAMOND
let dx = (px - py) >> 1
let diamondIndex = shapeOffset + (((px + py) >> 1) *
sw)
putPixel((squareSize / 2 + dx) + diamondIndex, 255, 255,
255)
putPixel((squareSize / 2 - dx) + diamondIndex, 255, 255,
255)
}
Iterative Dimetric cube (2025)

A tiny way to draw an "isometric" (dimetric)
cube in an iterative fashion with a single loop, all integers with
an integer variant of HAKMEM
149 (so called Minsky circle) display hack. (Sin / Cos
approximation)
It derive out of a way to draw a hexagon with the Minsky
algorithm (related
?) , the cube is actually a hexagon that is filled and
shaded.

the algorithm can be used to render a fractured cube as well
let sw = 512
let sh = 512
let r = 127 // cube size (loop shifts must be adapted as well if
modified)
let hr = r >> 1
let l = 1024 // try 720 etc. for a fractured cube
let y = r // can be 0
let x = frameCount
let o = width / 2 - r + (-hr + sh / 2) * sw
for (let i = 0; i < l; i += 1) {
y += x >> 7
x -= y >> 7 // increasing shift value "extrude" the
cube (should be accompanied by an increase of "l" as well)
y -= i & 1 // hexagon
let c = 0
// face detection & shade
let dx = (r - x) >> 1
if ((hr - y) > abs(dx)) {
c = 255
} else if (dx >= 0) {
c = 192
} else {
c = 92
}
let index = (o + x + y * width) * 4
putPixel(index, c)
}
HAKMEM 149 line algorithm (2025)
The HAKMEM
149 algorithm (an all integers CORDIC sin / cos
approximation) can be used for an angle-based line drawing
algorithm, i experimented with two approach, the obvious one is a
simple trigonometry approach with a progressively incremented
radius, this is simple and small especially if the input
coordinates is in polar
form. (e.g. don't have to compute the angle), it is also branch
less (except loops but they can be unrolled),
with a path the only needed input data would be the line length
(optional if fixed) and angle, the input data may use arbitrary
precision as a form of compression. Note that this algorithm don't
draw a perfect line, it has a small amount of overdraw. (angle
dependent)
The other approach use epicycle
which is another way to draw a line with two circles rotating in
opposite direction, this is much less efficient due to overdraw as
it approach the edges (it is a "collapsed" arc after all) but the
code remains almost as simple and small, biggest advantage of this
approach is that the line can morph into a curve with different
HAKMEM weight, this easily provide a way to stylize paths and it
can be used as a way to interpolate for animations etc.
Here is the code (p5js) for the trigonometry based HAKMEM 149
line drawing algorithm:
function hakmem149_line(x1, y1, x2,
y2) {
let precision = 8
// compute line length; can be precomputed / given as
input
let dx = x2 - x1
let dy = y2 - y1
let len = sqrt(dx * dx + dy * dy) | 0
if (len === 0) return
// get angle between two points; costly but unneeded if
input is polar
let angleRadian = getAngle(x1, y1, x2, y2)
// compute how much iterations is needed for some cycles
let fullCycle = 2 * PI * (1 << precision)
let angle = (angleRadian * (fullCycle >> 1) / Math.PI)
| 0
// adjust increment vector; can be precomputed (RAM costly)
or directly used as input to bypass computation
let x0 = 1 << (precision << 1)
let y0 = 0
for (let i = 0; i <= angle; i += 1) {
x0 -= y0 >> precision
y0 += x0 >> precision
// increase precision (increase cycle shift by 1
if used)
//y0 += x0 >> (precision - 1)
//x0 -= y0 >> precision
}
// downscale to get fixed point HAKMEM values
let xi = x0 >> precision
let yi = y0 >> precision
// drawing offset
let x = x1 << precision
let y = y1 << precision
for (let i = 0; i < len; i += 1) {
putPixel(x >> precision, y >>
precision, 255)
x += xi
y += yi
}
}Here is the code of the epicycle based HAKMEM 149 stylized
line drawing algorithm:
function hakmem149_line(x1, y1, x2,
y2) {
let precision = 10 // hakmem 149 shift
// compute line length; can be precomputed / given as
input
let dx = x2 - x1
let dy = y2 - y1
let len = sqrt((x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 -
y2))
if (len === 0) return
// prepare circles (radii)
let ml = len << precision
// ex0 and ex1 can be scaled dis-proportionally (such as :
x0 * 1.75 and x1 * 0.25) to "bend" the line (the half circle
appear)
let ex0 = ml
let ey0 = 0
// compute how much iterations is needed for some cycles
let circleFullCycle = 2 * PI * (1 << precision)
let circleHalfCycle = circleFullCycle >> 1
let circleQuarterCycle = circleHalfCycle >> 1
// get angle between two points; costly but unneeded if
input is polar
let angleRadian = getAngle(x1, y1, x2, y2)
let angle = angleRadian * circleHalfCycle / PI | 0
// adjust initial phase; can be precomputed but a bit RAM
costly to do so
for (let i = 0; i <= angle; i += 1) {
ex0 -= ey0 >> precision
ey0 += ex0 >> precision
}
let ex1 = ex0
let ey1 = ey0
// rotate the two circle over a quarter cycle; this produce
a quarter of a circle that is collapsed to a line due to
cancellation
for (let i = 0; i <= circleQuarterCycle; i +=
1) {
// cancel and downscale to get final
coordinates
let x = ex0 + ex1 >> (precision + 1)
let y = ey0 + ey1 >> (precision + 1)
// first circle
ex0 += ey0 >> precision
ey0 -= ex0 >> precision
// second circle with opposite rotation
ex1 -= ey1 >> precision
ey1 += ex1 >> precision
// add draw offset then draw
putPixel(x1 + x, y1 + y, 255)
}
}Note that this code use a quarter of a circle as an
optimization to have less overdraw, using half of a circle may be
more adequate for a stylized line, the only change is to use the
half cycle iteration constant with a mid line drawing offset, the
line length should also be divided by two.
Different HAKMEM weights (ex0, ey0, ex1,
ey1) can be used to stylize the line.
Here is the getAngle function for completion (not
needed with polar input):
function getAngle(x1, y1, x2, y2)
{
let dx = x2 - x1
let dy = y2 - y1
let magAB = sqrt(dx * dx + dy * dy)
let cosineTheta = dx / magAB
let angle = acos(cosineTheta)
if (dy < 0) {
angle = 2 * Math.PI - angle
}
return angle
}Rendering examples of a Hilbert curve
drawn with the epicycle version in an additive way to show the
overdraw:

collapsed quarter circle version, note that the
overdraw increase as the line end

half circle version, the overdraw increase at
it approach edges

stylized sample with disproportionate HAKMEM
weights

another stylized sample
Rendering example of a recursive tree drawn with the epicycle
line algorithm in an additive way and with varying weight as height
increase:

What is the advantage of these algorithms versus standard
algorithms ?
The epicycle approach may be of interest as a small / flexible
way to interpolate or stylize a line in few instructions without
div / mul nor floating-points arithmetic, it may be specifically
efficient on ARM CPUs. (shift + arithmetic as a single
instruction)
The simple trigonometry based approach has a more dubious use
case as the Bresenham
line or even a
fixed point line algorithm may be a better approach on most
CPUs to get maximum efficiency for simple lines in term of quality
(pixel-perfect) / speed, a
recursive subdivision approach may be best for code size, they
moreover have anti-aliased variants which the HAKMEM 149 algorithm
lacks.
The trigonometry based HAKMEM 149 approach may still be
of interest when the input is all polar and may be efficient on CPU
architectures such as ARM where a shift and addition / subtraction
can be done as a single instruction, the line setup can be
incredibly minimal with precomputation (or polar inputs) which
result in a single lookup and few arithmetic operations per line
and ~4 instructions per iteration at most on ARM, it is similar to
the standard fixed point line drawing algorithm (DDA)
with a slightly different setup. (polar vs Cartesian)
The common advantage is that rotation is almost free since it
is "bundled" into the algorithm !
HAKMEM 149 quad rasterizer / sprite scaler + rotation (2025)
A quad rasterizer can be easily done as an extension to the
line algorithm, a very simple square / rectangle extension is to
draw a second perpendicular line as the first line is iterated
:
function drawQuad(x1, y1, len,
angleRadian) {
let precision = 8
// compute how much iterations is needed for some cycles
let fullCycle = 2 * PI * (1 << precision)
let angle = angleRadian * (fullCycle >> 1) / PI |
0
// adjust increment vector; can be precomputed or used as
input instead of angle
let x0 = 1 << (precision << 1)
let y0 = 0
for (let i = 0; i <= angle; i += 1) {
x0 -= y0 >> precision
y0 += x0 >> precision
}
// downscale to get fixed point HAKMEM values
let x0n = x0 >> precision
let y0n = y0 >> precision
// compute center of rotation offset
let ox = ((x0n + y0n) >> 1) * len
let oy = ((y0n - x0n) >> 1) * len
// offset to rotate around center point
let ix = (x1 << precision) - ox
let iy = (y1 << precision) - oy
for (let i = 0; i < len; i += 1) {
// perpendicular line; quad fill
let jx = ix >> precision
let jy = iy
for (let j = 0; j < len; j += 1) {
// RGB gradient (unoptimized)
let r = (i / len) * 255
let g = ((len - i) / len) * ((len -
j) / len) * 255
let b = (j / len) * 255
// overdraw to fill forward mapping
gaps: (x,y) and (x + 1, y)
putPixel2(jx, jy >> precision,
r, g, b)
// perpendicular iteration
jx += y0n
jy -= x0n
}
ix += x0n
iy += y0n
}
}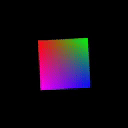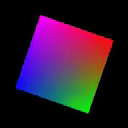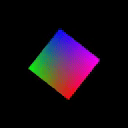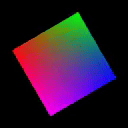
This support arbitrary rotation and scaling of the quad shape
with few additional code, it still benefit from the advantages of
the line algorithm on specific hardware.
Note : This is not a perfect way to rasterize a quad as it
produce gaps and overlaps / overdraw due to the line / mapping
approach, they can be an issue for things like blending, still an
okay small extension of the line algorithm, to fix the gaps i chose
to allow more overdraw by drawing two pixels at a time which is
cheap to do code wise. Another easy / small approach to fix the
gaps is to use smaller increments with more iterations to avoid any
misses, still produce overdraw though.
Note : Overdraw can be avoided by checking if the pixel has
been written, this is costly though.
A quad rasterizer with texture support is now easy by adding a
texture lookup (linear fetch !), an easy extension to draw scaled /
rotated sprites
(affine
mapping; billboarding)
:
function drawQuad(x1, y1, len,
angleRadian) {
let precision = 8
// compute how much iterations is needed for some cycles
let fullCycle = 2 * PI * (1 << precision)
let angle = angleRadian * (fullCycle >> 1) / PI |
0
// adjust increment vector; can be precomputed or used as
input instead of angle
let x0 = 1 << (precision << 1)
let y0 = 0
for (let i = 0; i <= angle; i += 1) {
x0 -= y0 >> precision
y0 += x0 >> precision
}
// downscale to get fixed point HAKMEM values
let x0n = x0 >> precision
let y0n = y0 >> precision
// compute center of rotation offset
let ox = ((x0n + y0n) >> 1) * len
let oy = ((y0n - x0n) >> 1) * len
// offset to rotate around center point
let ix = (x1 << precision) - ox
let iy = (y1 << precision) - oy
// texture lookup fixed point constants (can be
precomputed)
let reciprocalPrecision = 16 // decorrelated from
"precision" to represent small fractional steps
let reciprocalScaleFactor = 1 <<
reciprocalPrecision
let reciprocalLength = (reciprocalScaleFactor / len) | 0
// fixed point per‐pixel texture coordinates increments
let txi = tex.width * reciprocalLength
let tyi = tex.height * reciprocalLength
let tx = 0
for (let i = 0; i < len; i += 1) {
// perpendicular line; quad fill
let jx = ix >> precision
let jy = iy
// texture fetch init
let tpx = (tx >> reciprocalPrecision &
(tex.width - 1)) << 2
let ty = 0
for (let j = 0; j < len; j += 1) {
// texture lookup
let tpy = ty >>>
reciprocalPrecision & (tex.height - 1)
let col = getPixel(tex, tpx, tpy) //
fetch texture data
// draw
putPixel2(jx >> precision, jy
>> precision, col)
// perpendicular iteration
jx += y0n
jy -= x0n
ty -= tyi // decrement so that an
angle of 0 show the correct orientation
}
ix += x0n
iy += y0n
tx += txi
}
}
May still have room for speed / size optimizations on some
specific CPUs such as loop unrolling, bundling iterations as two
words etc.
Some easy paper / sheet like distorted / "curved
surfaces" (note : not accurate 3D curvatures) can be made by
disrupting the line coords iteration such as adding the loop index
to them. (try
jx += y0n + i; jy -= x0n + i;)This series of step from a line algorithm up to a quad
rasterizer can be seen as how sprite
based hardware progressed in the 80s / 90s (some of them may use an
inverse mapping approach for efficiency though) up to "distorted
quads" support on 3DO / Sega Saturn /
arcade (Sega
Model series and Namco System 21
/ 22),
this peaked with the quadratic texture mapping / non planar quads
of the Nvidia NV1
GPU, these last 3D focused approaches provided very small
amount of advantages though and are mostly obsolete now, they were
replaced by triangles as it was more elementary (always planar
etc.) than a quad with an efficient rasterization process,
triangles rasterizer originally started from a scan-line
based approach then switched to a Barycentric
/ tiled approach on modern GPUs. A barycentric approach also works to
rasterize quads.
What about more degrees of freedom ? (pitch /
yaw)
Code above can be naturally extended towards a 1-point /
2-point equiangular 3D quad by adding the missing degrees
of freedom (pitch / yaw), this may inflate the code and makes
the HAKMEM approach obsolete though as it would be more manageable
with something like a lookup table (or direct trigonometry calls)
by then.
An extension that is still small to add is the pitch component
(which squeeze the quad on the y axis) by replacing some of the
code above and adding a pitchAngleRadian argument :
// compute y iteration step for
pitch
let sinp = sin(pitchAngleRadian) * (1 << precision) | 0 //
can still use the HAKMEM algorithm but a lookup table may be better
by then
let x0np = (x0n * sinp) >> precision
let y0np = (y0n * sinp) >> precision
// compute center of rotation offset
let ox = ((x0n + y0n) >> 1) * len // unchanged
let oy = (((y0np - x0np)) >> 1) * len
...
for (let i = 0; i < len; i += 1) {
...
for (let j = 0; j < len; j += 1) {
...
jy -= x0np
...
}
...
iy += y0np
...
}
The only component left for a full
3D equiangular quad now is the yaw component
which can be added in the same fashion (or hacked by using the
pitch code on X axis; this adds constrains), note that some kind of
weak perspective projection must be added to makes all this
"3D", it is now out of context though as this adds quite a bit of
code...
Using affine mapping + quads (planar) over
triangles
provide a slight advantage (data reduction, less texture
distortion) in some context although texture distortion is easily
fixed with perspective correct interpolation.

a small
2.5D extension by stacking multiple planes on the Y axis with
heightmap / colormap lookup
Forward mapping vs inverse mapping
The quad rasterizer above use a
forward mapping approach, the loop iterate from the source
image in a linear fashion and map to output space (linear fetch and
random write), forward mapping is known to have disadvantages such
as gaps and overlaps depending on specific spatial transform
function, they were addressed above by tolerating overdraw which is
reasonable speed / quality wise given the goal and the simplicity
of the transform but it may become a bigger issue if accuracy is
expected or when the algorithm is extended to distorted sprites or
with special drawing modes such as blending. (see 3DO / Sega Saturn)
There is accurate ways to fix the gaps and overlaps (rectangle
to quad approach) but they are challenging to implement and out
of scope.
Inverse /
backward mapping is the inverse process (random fetch, linear
write) and map pixels from destination to source, it is a common
approach which does not have much issues.
Forward mapping is still interesting with simple transforms as
it may be more straightforward (less code), it may also provide
some speed advantages in some cases (linear fetch / random write,
cache friendliness ?), an interesting demonstration of forward
mapping speed advantage can be seen in the state of art
implementation of the Nvidia NV1 GPU (see TECHOVER.PDF
in nv1-sdk) which show that it may be up to two times faster
compared to inverse mapping in specific use cases, also has
space-wise advantages.
HAKMEM 149 rotozoom (2025)
For completion here is an inverse mapping approach for a
screen wide HAKMEM 149 based rotozoom :
function rotozoom(x1, y1, scal,
angleRadian) {
let precision = 8
// compute how much iterations is needed for some cycles
let fullCycle = 2 * PI * (1 << precision)
let angle = angleRadian * (fullCycle >> 1) / PI |
0
// adjust increment vector; can be precomputed or used as
input instead of angle
// increment also scaled here
let x0 = (1 << (precision << 1)) + (scal
<< precision)
let y0 = 0
for (let i = 0; i <= angle; i += 1) {
x0 -= y0 >> precision
y0 += x0 >> precision
}
// downscale to get fixed point HAKMEM values
let x0n = x0 >> precision
let y0n = y0 >> precision
// compute center of rotation offset
let ox = ((x0n + y0n) >> 1) * width
let oy = ((y0n - x0n) >> 1) * height
// offset to rotate around center point
let ix = (x1 << precision) - ox
let iy = (y1 << precision) - oy
for (let i = 0; i < width; i += 1) {
// perpendicular line
let jx = ix
let jy = iy
for (let j = 0; j < height; j += 1) {
// texture lookup
let tpx = (jx >> precision) &
(tex.width - 1)
let tpy = (jy >> precision) &
(tex.height - 1)
let col = getPixel(tex, tpx, tpy) //
fetch texture data
putPixel(i, j, col)
// perpendicular iteration
jx += y0n
jy -= x0n
}
ix += x0n
iy += y0n
}
}The downscale and angle computation can be shortened to few
instructions by running the HAKMEM add / sub per frame and using x0
/ y0 as input directly.

Inverse mapping in this particular case is
straightforward, efficient drawing of a single quad require loop
start / end and UV adjustments though.
HAKMEM 149 fractal (2025)
HAKMEM
149 is an algorithm (a CORDIC sin / cos
approximation) i tinker with since ~2020, i discussed this
algorithm many times here and on some pages along with the
derived
fractal i iterated on for some years, here is a minimal 512x512
Fractal version which produce nice result out of the box. (without
offsetting)

HAKMEM 149 fractal produced by the code
below
let x = -1
let y = 0
function draw() {
let iterations = 4e5
for (let i = 0; i < iterations; i += 1) {
x += y >>> 2
y -= x >> 1
x += y >> 2
putPixel(x >>> 23, y >>> 23,
255)
}
}What is going on ? I don't really know but it is pretty
similar to the way an Iterated
Function System / chaotic
maps works i guess.
The algorithm works in a 32 bits range (also works at lower
range but there may be precision loss) with a huge seed coordinate,
the iteration is then pretty similar to the integer version
of HAKMEM
149 (with ramped up precision) except that it use unsigned
right shifts in this case instead of signed ones to spice the
iteration up, this force interesting patterns without an offset
pass, the final shifts is a downscale pass to pack it minimally to
a 512x512 display window by using the last bits of the coordinates,
unsigned shifts ensure it fit into the 512x512 boundaries.
These patterns can also be produced with the low precision
skewed HAKMEM
149 which require less instructions :

a less precise HAKMEM 149 produce a slightly
skewed version
let x = -1
let y = 0
function draw() {
let iterations = 4e5
for (let i = 0; i < iterations; i += 1) {
x += y >>> 3
y -= x >>> 3
putPixel(x >>> 23, y >>> 23,
255)
}
}
Some notes :
- i don't know if someone did this in the 90s (or even 80s) but i have seen some 90s small intros with the same patterns, i didn't look at the code to confirm (they may be variation of some known chaotic maps such as Hopalong map), some recent ones also abuse variation of the HAKMEM 149 algorithm to produce nice real-time patterns, see also many intros by g0blinish that seem to use it, see this page for some other references, "Superhop" (ANTIC VOL. 8, NO. 4 / AUGUST 1989) looks quite similar !
- swapping iteration sign flip the image horizontally (when using signed shifts)
- rotate right instruction instead of a right shift makes it converge faster
- usage of signed shifts for the iteration works but you may have to add an offset pass (usually huge offset) to one of the coordinates to force the production of nice patterns
- different iteration shifts scale up / down the patterns, different shift ratio between x and y may produce skewed patterns
- different seeds produce different patterns
- the downscale method can be used to render other chaotic maps with small code, the only change is the coordinates iteration code usually
- drawing with an additive fashion (progressive; not just with an on / off pixel) reveal more details
- a horizontal seam may appears on some configuration due to the final unsigned shift on y coordinate, this can be solved by going for a signed shift instead and adding a vertical offset to center the image


with colors;
exponentially mapped based on iteration count; code



using logical operators; code


same as before but busier (see Apollonian)
back to top
